கல்வி ஆய்வியலில் தொகைசார் தரவுப் பகுப்பாய்வு
Quantitative Data Analysis in Educational Research
ஆக்கம்: கலாநிதி எப்.எம்.நவாஸ்தீன் சிரேஸ்ட விரிவுரையாளர் கல்விப் பீடம்இலங்கை திறந்த பல்கலைக்கழகம்1.0 அறிமுகம்
ஆய்வியல் செயன்முறையில் தரவு பகுப்பாய்வு முக்கியம் இடம் வகிக்கிறது. ஆய்வுக்கு எடுத்துக் கொள்ளப்பட்ட பிரச்சினையின் தன்மையினை விளங்கிக் கொள்ளவும், அதற்கேற்ப பொருத்தமான தீர்வுகளை கண்டறிவதற்கும் தரவுப் பகுப்பாய்வு தேவையாகின்றது. கல்விசார் ஆய்வுகளில் மட்டுமன்றி, எல்லா வகையான ஆய்வுகளிலும் இது முக்கியம் பெறுகிறது. ஆய்வாளர்கள், தமது ஆய்வு பிரச்சினைக்குரிய ஆய்வுக் குறிகோள்களுக்குப் பொருத்தமான தரவுகளை சேகரிப்பதுடன் மட்டுமன்றி, அவற்றை பொருத்தமான வகையில் பகுப்பாய்வு செய்யும் போதே ஆய்வுப்பிரச்சினை தொடர்பான அர்த்தமிகு தகவல்களையும், முடிவுகளையும் பெற முடியும். ஆய்வுகளில், தொகைசார் (Quantitative) பண்பறிசார் (Qualitative) ஆய்வுகள் மட்டுமன்றி, இரண்டும் கலந்த கலப்பு ஆய்வு (Mixed Methods) முறைகள் அண்மைகாலமாக குறிப்பாக கல்வித்துறையில் அதிகரித்து வருகின்றன. கல்வித் துறையில் ஆய்வுகளில் ஈடுபடுவோர் தரவுப்பகுப்பாய்வு முறைகளை அறிந்து வைத்து இருப்பது மிக முக்கியமாகும். எனவே, தரவு பகுப்பாய்வு பற்றி, குறிப்பாக, பொருத்தமான தொகை சார் தரவுப் பகுப்பாய்வு நுட்பங்களை எங்ஙனம் தெரிவு செய்வது என்பது தொடர்பாக இக்கட்டுரை ஆராய்கின்றது.
2.0 தரவு பகுப்பாய்வு என்றால் என்ன?
தரவு பகுப்பாய்வு என்பது சேகரித்த தரவை விவரிக்கவும் விளக்கவும், சுருக்கவும், மறுபரிசீலனை செய்யவும் மற்றும் மதிப்பீடு செய்யவும் புள்ளிவிவர மற்றும் / அல்லது தர்க்க நுட்பங்களை முறையாகப் பயன்படுத்துவதற்கான செயல்முறையாகும். இதன் மூலம் சேகரித்த தரவில் இருந்து அர்த்தபூர்வமான முடிவுகளை ஆய்வாளருக்கு பெற்றுக் கொள்ள முடிகிறது. தரவுப்பகுப்பாய்வு என்பது, சேகரித்த தரவுகளை பகுப்பாய்வுக்காக தயார்படுத்தல், பகுப்பாய்வைச் மேற்கொள்ளல், பெறுபேறுகளை அறிக்கையிடல், அவற்றை விளக்கிக்கூறல் போன்ற படிமுறைகளை கொண்டுள்ள ஒரு செயன்முறையாக உள்ளது.
தரவு பகுப்பாய்வில், தொகை சார் தரவு பகுப்பாய்வு, பண்புசார் தரவு பகுப்பாய்வு என இரு வகைகள் உள்ளன.
2.1 தொகைசார் தரவுப் பகுப்பாய்வு- (தரவு) மாறி (சார்ந்த மாறி, சுயாதீன மாறி) (Variables)
- தரவின் அளவிடை மட்டங்கள் (Scale of measurements)
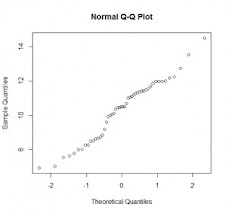
- தரவுத் தொகுதின் செவ்வன் பரம்பல் தன்மை (Normality of data set)
- மாறி- Variable
- மாறிலி- Constant
- சாரா மாறி (சுயாதீன மாறி).
- சார்ந்த மாறி (தங்கி மாறி),
|
மேலே
உள்ள உதாரணங்களில் எடுத்துக் காட்டப்பட்டது போல, உங்கள் ஆய்வினில்
உள்ள ஆய்வுக் குறிக்கோள்கள்/ ஆய்வு
வினாக்களில் உள்ள மாறிகள், சுயாதீன மாறி(கள்) சார்ந்த மாறி(கள்) என்பவற்றை அடையாளப்படுத்துங்கள்
|
- சேர்த்தி (Association)
- வேறுபாடுகள் (Differences)
- இணைபு (Correlation)
- பெயரளவு அல்லது வகைப்படுத்தல் மட்டம் (Nominal)
- வரிசைப்படுத்தல் மட்டம் (Ordinal)
- ஆயிடை அளவு மட்டம் (Interval)
- விகித அளவு மட்டம் (Ratio)
உதாரணம்: வகுப்பறையில் மாணவர்கள் ஆசிரியரின் கற்பித்தலில் பயன்படுத்திய நுட்பங்கள் பற்றி மாணவர்களாகிய உங்களது கருத்து யாது?
1. மிக நன்றன்று 2. நன்றன்று 3. ஓரளவு நன்று 4. நன்று 5. மிகவும் நன்று
இந்த நான்கு அளவிடை மட்டங்களை தரவுப் பகுப்பாய்வுக்காக
பின்வருமாறு இரு வகைகளில் பகுத்து நோக்குவர்.
- பெயரளவு அளவிடை மற்றும் வரிசை அளவிடை மாறிகள் – பின்னக தரவுகள் (Discrete Data)
- இடைவெளி மற்றும் ஆயிடை அளவிடை மாறிகள் – தொடர் தரவுகள் (Continuous Data)
தரவுத்தொகுதி செவ்வன் பரம்பல் பண்பினை பெறுகின்ற போது, ஆய்வாளர் புள்ளியல் சோதனைகளில் பரமான சோதனைகளை (Parametric test) தெரிவு செய்து அவற்றை பயன்படுத்திக் கொள்ள முடியும்.
தரவுத்தொகுதி செவ்வன் பரம்பல் பண்பினை பெற்றிராத போது பரமானமற்ற சோதனைகளை (Non-Parametric test) யே பயன்படுத்திக் கொள்ள முடியும்.
எனவே இதுவரை மாறிகள், மாறிகளின் அளவிடை மட்டங்கள், செவ்வன் பரம்பல் தன்மை ஆகியவற்றை விளங்கிக் கொண்டோம். இதன் பின்னர், எத்தகைய புள்ளியியல் சோதனைகளை, கணிப்பீடுகளை தரவுப் பகுப்பாய்வுக்காக தெரிவு செய்ய வேண்டும் என நோக்குவோம்.
2.2 தனித்த மாறிகளை பகுப்பாய்வு செய்தல் (Univariate Analysis)
ஏற்கனவே, தனித்த மாறி என்றால் என்ன என்பது தொடர்பாக விளக்கி உள்ளேன். சில வேளைகளில் எமது ஆய்வுகளின் குறிக்கோள்களில் தனித்த மாறி காணப்படும். இத்தகைய சந்தர்பங்களில் அதனது போக்கினையே உங்களால் விவரிக்க முடியும். இதன்போது வீதம், மீடிறன் பரம்பல் அட்டவணைகள், மையப் போக்கு அளவைகள் (கூட்டல் இடை, இடியம், ஆகாரம்), விலகல் அளவைகள் (மாறற்றிறன், நியம விலகல், வீச்சு ) போன்றன போதுமாக இருக்கும். பின்வரும் படத்தைப் பார்க்க;
Source: Creswell (2011:P183)
2.3.1 மாறிகள் பின்னகத் தரவுகளாக அமையும் போது
எமது தரவு தொகுதியில் உள்ள சுயாதீன மாறியும் (IV) சார்ந்த மாறியும் (DV) பின்னகத் தரவுகளாக (பெயரளவு , வரிசைத் தரவுகள்) அமையும் போது அவற்றுக்கிடையில் Association எனும் சேர்த்தி எவ்வாறு உள்ளது என்றே நாம் பகுப்பாய்வு செய்ய முடியும். இதன்போது. நாம் கைவர்க்க சோதனைகள் (Chi-Square Analysis) பை-குணகம் (Phi Coefficient) ஆகியவற்றையே பகுப்பாய்வுக்காக எடுத்துக் கொள்ள முடியும்.
2.3.2 சுயாதீன மாறிகள் மற்றும் சார்பு மாறிகள் இரண்டுமே தொடர் தரவுகளாக அமையும் போது:
எமது தரவு தொகுதியில் உள்ள சுயாதீன மாறியும் (IV) சார்ந்த மாறியும் (DV) தொடர் தரவுகளாக (இடைவெளி, விகித அளவிடைகளாக) அமையும் போது அவற்றுக்கிடையில் இணைபுகளை (Correlation) எவ்வாறு உள்ளது என்று நாம் பகுப்பாய்வு செய்ய முடியும். இதன்போது. நாம் பியர்சன் இணைபு குணகம் (Pearson Correlation Coefficient) பிற்செலவு பகுப்பாய்வு குணகம் (Regression Coefficient) போன்ற பரமான சோதனைகளை பகுப்பாய்வுக்காக தெரிவு செய்து கொள்ள முடியும்.
2.3.3 சுயாதீன மாறி பின்னகமாகவும் மற்றும் சார்பு மாறி தொடர் தரவாகவும் அமையும் போது:
எமது தரவு தொகுதியில் உள்ள சுயாதீன மாறி (IV) பின்னகமாக அமைந்து சார்ந்த மாறி (DV) தொடர் தரவாக (இடைவெளி, விகித அளவிடைகளாக) அமையும் போது அவற்றுக்கிடையில் வேறுபாடுகளை (Differences) நாம் கணிப்பீடு செய்யக் கூடியதாக இருக்கும். இதன் போது இரண்டு குழுக்களிடையே (ஆண்-பெண்) வேறுபாட்டை பார்க்க t-test எனும் பரமான சோதனையை செய்ய முடியும். இரண்டுக்கும் மேற்பட்ட குழுக்களிடையே வேறுபாடுகளை காண விரும்பின் (1AB, 1C, Type 2 பாடசாலைகள்) Analysis of Variance (ANOVA), Analysis of Covariance போன்ற பரமான சோதனைகளை பகுப்பாய்வுக்காக தெரிவு செய்து கொள்ள முடியும்.
2.3.4 சுயாதீன மாறி தொடர் தரவாகவும் மற்றும் சார்பு மாறி பின்னகமாகவும் அமையும் போது:
எமது தரவு தொகுதியில் உள்ள சுயாதீன மாறி (IV) தொடர் தரவாக (இடைவெளி, விகித அளவிடைகளாக) சார்ந்த மாறி (DV) பின்னகமாக அமைந்து அமையும் போது அவற்றுக்கிடையில் நேர்கோட்டு தொடர்பினை கணிப்பிடக் கூடியதாக இருக்கும் இதன் போது ஏகபரிமாணப் பிரித்துக்காட்டி எனும் Discriminant Analysis பரமான சோதனையினை பகுப்பாய்வுக்காக தெரிவு செய்து கொள்ள முடியும்.
2.4.1 சுயாதீன மாறிகள் மற்றும் சார்பு மாறிகள் இரண்டுமே தொடர் தரவுகளாக அமையும் போது பரமானமற்ற சோதனைகள் :
எமது தரவு தொகுதியில் உள்ள சுயாதீன மாறியும் (IV) சார்ந்த மாறியும் (DV) தொடர் தரவுகளாக (இடைவெளி, விகித அளவிடைகளாக) அமையும் போது அவற்றுக்கிடையில் இணைபுகளை (Correlation) எவ்வாறு உள்ளது என்று நாம் பகுப்பாய்வு செய்ய முடியும். இதன்போது, எமது தரவுத் தொகுதி சாதாரண பரம்பல் தன்மையினை பெறாத போது பரமானமற்ற சோதனைகளையே நாம் தெரிவு செய்ய வேண்டும். இதற்காக Spearman Rho அல்லது Kendall's Tau சோதனைகளை நாம் தெரிவு செய்து கொள்ள முடியும்.
2.4.2 சுயாதீன மாறி பின்னகமாகவும் மற்றும் சார்பு மாறி தொடர் தரவாகவும் அமையும் போது பரமானமற்ற சோதனைகள் :
எமது தரவு தொகுதியில் உள்ள சுயாதீன மாறி (IV) பின்னகமாக அமைந்து சார்ந்த மாறி (DV) தொடர் தரவாக (இடைவெளி, விகித அளவிடைகளாக) அமையும் போது அவற்றுக்கிடையில் வேறுபாடுகளை (Differences) நாம் கணிப்பீடு செய்யக் கூடியதாக இருக்கும். இதன்போது, எமது தரவுத் தொகுதி சாதாரண பரம்பல் தன்மையினை பெறாத போது, பரமானமற்ற சோதனைகளையே நாம் தெரிவு செய்ய வேண்டும். இதற்காக, Mann-Whitney U test, Kruskall–Wallis Test போன்ற பரமானமற்ற சோதனைகளை பகுப்பாய்வுக்காக தெரிவு செய்து கொள்ள முடியும்.
2.4.3 சுயாதீன மாறி தொடர் தரவாகவும் மற்றும் சார்பு மாறி பின்னகமாகவும் அமையும் போது பரமானமற்ற சோதனைகள்:
எமது தரவு தொகுதியில் உள்ள சுயாதீன மாறி (IV) தொடர் தரவாக (இடைவெளி, விகித அளவிடைகளாக) சார்ந்த மாறி (DV) பின்னகமாக அமைந்து அமையும் போது அவற்றுக்கிடையில் நேர்கோட்டு தொடர்பினை கணிப்பிடக் கூடியதாக இருக்கும் இதன்போது, எமது தரவுத் தொகுதி சாதாரண பரம்பல் தன்மையினை பெறாத போது, பரமானமற்ற சோதனைகளையே நாம் தெரிவு செய்ய வேண்டும். இதற்காக, Point Biserial Correlation எனும் சோதனையினை பகுப்பாய்வுக்காக தெரிவு செய்து கொள்ள முடியும்.
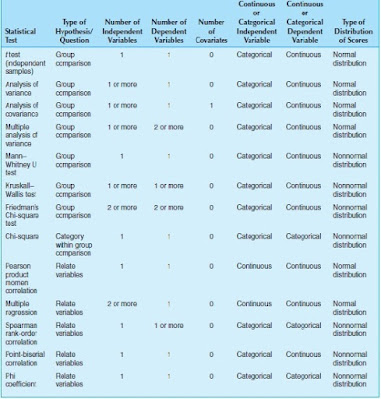
நாம் இதுவரை நோக்கிய பரமான சோதனைகள், பாரமானமற்ற சோதனைகளின் தெரிவினை பின்வரும் படத்தில் காணலாம்.
Source: Creswell (2011:P183)
மேலும், நாம் இதுவரை எடுத்து நோக்கிய விடயங்களில் தரவுகள் சாதாரண பரம்பலில் அமையும் போது மற்றும் சாதாரண பரம்பல் பெறாத வேளைகளில் எத்தகைய பகுப்பாய்வு முறைகளை/சோதனைகளை நாம் தெரிவு செய்ய வேண்டும் என்பதனை பின்வரும் அட்டவணையில் கண்டு கொள்ளக் கூடியதாக உள்ளது.
சிறியளவிலான தொகைசார் தரவுகளை பகுப்பாய்வுக்கு உட்படுத்தும்போது அவற்றை புள்ளியியல் நுட்பமுறைகள், வாய்ப்பாடுகள் ஆகியவற்றை பயன்படுத்தி தரவு பகுப்பாய்வினை பயன்படுத்தி அட்டவணைப்படுத்தல், படங்களாக முன்வைத்தல், சேர்த்தி தன்மை, இணைபு தன்மைகள், வேறுபாடுகளை நாம் சுயமாக கணித்து கொள்ள முடியுமாக இருக்கும். ஆனால் தரவுகள் அதிகமாக உள்ள போது, அவற்றை எம்மால் கையாள முடியாமல் போகும். வேகமாக வளர்ச்சியடைந்து தகவல் தொழினுட்பம் காரணமாக தரவுப் பகுப்பாய்வுகள் இலகுவாக மேற்கொள்ளக் கூடிய வகையில் பற்பல மென்பொருள்கள் (Software) பயன்பாட்டிற்கு நாளாந்தம் வந்த வண்ணம் உள்ளன. இவற்றுள் Microsoft Excel முதற்கொண்டு SPSS, AMOS, Stata, SAS, R, MATLAB, JMP, Python என பல நூற்றுக்கணக்கான மென்பொருள்கள் பாவனையில் உள்ளன. கல்வி மற்றும் சமுக விஞ்ஞான துறைகளில் Microsoft Excel, SPSS, AMOS, Stata, SAS, என்பன பயன்பாட்டில் உள்ளன. SPSS யினை கொள்வனவு செய்து பயன்படுத்துவது சிரமம் உள்ளவர்கள் அதற்கு நிகரான JASP, Jamovi, மற்றும் Gnu PSPP போன்ற இலவச மென்பொருள்களை ஆய்வாளர்கள் பயன்படுத்துகின்றனர்.